개발 블로그

문제 링크 : www.acmicpc.net/problem/7576

문제

철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자 모양 상자의 칸에 하나씩 넣어서 창고에 보관한다. 

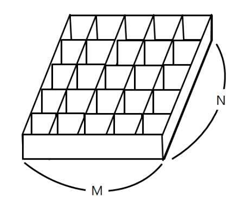
창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토의 인접한 곳은 왼쪽, 오른쪽, 앞, 뒤 네 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지, 그 최소 일수를 알고 싶어 한다.

토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.

입력

첫 줄에는 상자의 크기를 나타내는 두 정수 M,N이 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M,N ≤ 1,000 이다. 둘째 줄부터는 하나의 상자에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 상자에 담긴 토마토의 정보가 주어진다. 하나의 줄에는 상자 가로줄에 들어있는 토마토의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다.

토마토가 하나 이상 있는 경우만 입력으로 주어진다.

출력

여러분은 토마토가 모두 익을 때까지의 최소 날짜를 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.

접근 방법

fromStart[][]을 이용해서 방문 여부와 동시에 토마토가 익을때까지 걸린 day수를 저장한다.

처음 배열을 입력할 때 1인 경우를 queue에 push 하고,

입력받음과 동시에 1인 칸의 수(int start)와 -1인 칸의 수(int minu)를 카운트한다.

이는 마지막에 영향받아 익은 토마토 수(int chk)와의 덧셈연산을 통해 안 익은 토마토가 남았는지를 검사하는데에 이용한다.

이 외에 나머지는 일반 BFS와 같은 로직이다.

주의할 점

1)

if(fromStart[nr]ncc] > fromStart[r][c]+1) 인 경우에만 fromStart[nr][nc] 를 fromStart[r][c]+1로 갱신해줘야하나 싶었는데, 

어짜피 fromStart[nr][nc]에 값이 저장되는 그 순간에 그게 필요한 최소 day 수 이므로 체크할 필요가 없이

if(fromStart[nr][nc] == 0 && map[nr][nc]==0) 인 조건만 만족하면 fromStart[nr][nc] 를 갱신하면 된다. 

2)

가로 칸의 수는 M(col), 세로 칸의 수는 N(row) 이다.

3)

2<=N,M<=1000이고 상하좌우 검사해야해서 map[1002][1002], fromStart[1002][1002] 로 선언해야 했는데

nr<0 || nr >=N || nc<0 || nc >=M  로 범위 검사를 하니 1000으로 선언해도 된다.

#include <iostream>
#include <queue>
#include <utility>

using namespace std;


int map[1000][1000];
int fromStart[1000][1000];

int M;  //가로 col
int N;  //세로 row
int nr, nc;
int start = 0, minu=0;
int r, c;

//위 오 아 왼
int dr[4] = {-1, 0, 1, 0};
int dc[4] = {0, 1, 0, -1};

queue<pair<int, int>> que;

void BFS(){
    
    while(!que.empty()){
   
        r = que.front().first;
        c = que.front().second;
        que.pop();
        
        for(int i = 0; i<4; i++){
            
            nr = r + dr[i];
            nc = c + dc[i];
            
            if(nr<0 || nr >=N || nc<0 || nc >=M || map[nr][nc]==-1) continue;    //map -1이면 토마토 없음
            
            if(fromStart[nr][nc]==0 && map[nr][nc]==0){ //방문 안 했고 안 익은 토마토 있으면
                fromStart[nr][nc] = fromStart[r][c]+1;
                que.push(make_pair(nr,nc));
            }
        }
    }
}


int main(){
    
    cin >> M >> N;
    
    for(int i = 0 ;i <N; i++){
        for(int j = 0; j<M; j++){
            fromStart[i][j] = 0;        //visit 여부 & 해당 칸 토마토가 익기까지 day 수 저장
            
            cin >> map[i][j];
            if(map[i][j] == 1){
                que.push(make_pair(i,j));
                start++;                            //start는 맨 처음 익은 토마토 수
            }
            else if(map[i][j] == -1) minu++;        //minu는 토마토 없는 칸 수
        }
    }
    
    BFS();
    
    int chk = 0;
    for(int i = 0; i<N; i++){
        for(int j = 0; j<M; j++){
            if(fromStart[i][j]!=0) chk++;            //방문 안한곳 있으면 -1 출력하기 위함
        }
    }
   
    if(chk+start+minu==M*N) cout << fromStart[r][c];
    else cout << -1;
    
    return 0;
}

문제 링크 : www.acmicpc.net/problem/2667

문제

<그림 1>과 같이 정사각형 모양의 지도가 있다. 1은 집이 있는 곳을, 0은 집이 없는 곳을 나타낸다. 철수는 이 지도를 가지고 연결된 집의 모임인 단지를 정의하고, 단지에 번호를 붙이려 한다. 여기서 연결되었다는 것은 어떤 집이 좌우, 혹은 아래위로 다른 집이 있는 경우를 말한다. 대각선상에 집이 있는 경우는 연결된 것이 아니다. <그림 2>는 <그림 1>을 단지별로 번호를 붙인 것이다. 지도를 입력하여 단지수를 출력하고, 각 단지에 속하는 집의 수를 오름차순으로 정렬하여 출력하는 프로그램을 작성하시오.

입력

첫 번째 줄에는 지도의 크기 N(정사각형이므로 가로와 세로의 크기는 같으며 5≤N≤25)이 입력되고, 그 다음 N줄에는 각각 N개의 자료(0혹은 1)가 입력된다.

출력

첫 번째 줄에는 총 단지수를 출력하시오. 그리고 각 단지내 집의 수를 오름차순으로 정렬하여 한 줄에 하나씩 출력하시오.

접근 방법

map[0][0] ~ map[N-1][N-1] 까지 돌면서 방문하지 않은 곳에서 dfs를 호출한다. 호출하기 전에 cnt를 1로 초기화 한 뒤, dfs 함수 안에서 재귀로 dfs가 재호출 될 때마다 연결된 단지로 전진한 것이므로 cnt를 1씩 증가해준다. 처음에 호출한 dfs가 끝나면 cnt를 cntVec안에 push 해서 마지막에 출력할 수 있도록 저장하고, 단지 그룹 1개를 다 탐색한 것이므로 res를 1 증가시킨다.

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>

using namespace std;

int map[25][25];
int visited[25][25];
vector<int> cntVec;

//위 오 아 왼
int dr[4] = {-1,0,1,0};
int dc[4] = {0,1,0,-1};
int N;
int cnt;

void dfs(int r, int c){

    for(int i = 0; i<4; i++){
        
        int nr = r + dr[i];
        int nc = c + dc[i];
        
        if(nr>=N || nr<0 || nc>=N || nc<0) continue;
        
        if(visited[nr][nc]==0 && map[nr][nc]==1){   //방문 안했고 집이 있으면
            visited[nr][nc] = 1;                    //방문했다고 표시하고
            cnt+=1;                                 //집 개수 세기
            dfs(nr,nc);
        }
    }
 
}


int main(){
    
    int res=0;
    
    cin >> N;
    string str;
    
    for(int i = 0; i<N; i++){
        cin >> str;
        for(int j = 0; j<str.length(); j++){            //입력 주의
            visited[i][j] = 0;
            
            if(str[j] == '1'){
                map[i][j] = 1;
            }
            else map[i][j] = 0;
        }
    }
    
    
    for(int i = 0; i<N; i++){
        for(int j = 0; j<N; j++){
            
            if(map[i][j]==1 && visited[i][j]==0){
                visited[i][j] = 1;
                cnt = 1;                        //처음은 시작점 포함하므로 1로 초기화
                dfs(i,j);
                cntVec.push_back(cnt);
                res++;                          //단지 그룹 1개 탐색 끝남
            }
        }
    }
    
    sort(cntVec.begin(), cntVec.end());
    cout << res << "\n";
    
    for(int i = 0; i<cntVec.size(); i++){
        cout << cntVec[i] << "\n";
    }

    return 0;
}

문제 링크 : www.acmicpc.net/problem/13023

문제

BOJ 알고리즘 캠프에는 총 N명이 참가하고 있다. 사람들은 0번부터 N-1번으로 번호가 매겨져 있고, 일부 사람들은 친구이다.

오늘은 다음과 같은 친구 관계를 가진 사람 A, B, C, D, E가 존재하는지 구해보려고 한다.

• A는 B와 친구다.
• B는 C와 친구다.
• C는 D와 친구다.
• D는 E와 친구다.

위와 같은 친구 관계가 존재하는지 안하는지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 사람의 수 N (5 ≤ N ≤ 2000)과 친구 관계의 수 M (1 ≤ M ≤ 2000)이 주어진다.

둘째 줄부터 M개의 줄에는 정수 a와 b가 주어지며, a와 b가 친구라는 뜻이다. (0 ≤ a, b ≤ N-1, a ≠ b) 같은 친구 관계가 두 번 이상 주어지는 경우는 없다.

출력

문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.

접근 방법

문제에서 아래의 조건이 주어졌다.

• A는 B와 친구다.
• B는 C와 친구다.
• C는 D와 친구다.
• D는 E와 친구다.

이는 N명에게 연결된 친구를 각각 dfs 로 타고 가봤을 때, 그 깊이가 4가 되는게 있는지를 확인해서 풀 수 있다. 

벡터 배열을 이용해 양방향으로 친구 관계를 연결해주고 벡터 배열 크기만큼 dfs를 돌린다.

첫번째와 두번째 방법은 같으나

첫번째는 flag 변수와 return; 으로 dfs를 중단해보았고

두번째는 exit(0); 으로 즉시 종료를 해보았다.

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

int visited[2000] = {0};
vector<int> vecArr[2000];
bool flag = false;

void dfs(int start, int depth){
    
    visited[start] = 1;
    
    if(depth==4){
        flag = true;				//더 이상 dfs 실행 안 되게 함. 
        cout << 1 << "\n";
        return;
    }
    
    for(int i = 0; i<vecArr[start].size(); i++){
        if(visited[vecArr[start][i]]==0 && !flag){		//위에서 flag=true 됐으면 조건문 실행 x
            dfs(vecArr[start][i], depth+1);				//타고 들어갈 때마다 depth 증가
        }
    }

    visited[start] = 0;
    
}




int main(){

    queue<int> que;
    
    int N,M;
    cin >> N >> M;
    
    int a, b;
    for(int i = 0; i<M; i++){			//관계 양 방향 연결 (벡터 배열 사용)
        cin >> a >> b;
        
        vecArr[a].push_back(b);
        vecArr[b].push_back(a);
        
    }
    
    
    for(int i = 0; i<N; i++){
        dfs(i,0);
    }
    
    if(!flag) cout << 0;				//다 탐색 했는데 깊이가 4 된 경우 없으면 0 출력.
    
    return 0;
}

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

int visited[2000] = {0};
vector<int> vecArr[2000];

void dfs(int start, int depth){
    
    visited[start] = 1;
    
    if(depth==4){
        cout << 1 << "\n";
        exit(0);						//즉시 종료. 
    }
    
    
    for(int i = 0; i<vecArr[start].size(); i++){
        if(visited[vecArr[start][i]]==0){
            dfs(vecArr[start][i], depth+1);
        }
    }
    
    visited[start] = 0;
    
}




int main(){

    queue<int> que;
    
    int N,M;
    cin >> N >> M;
    
    int a, b;
    for(int i = 0; i<M; i++){
        cin >> a >> b;
        
        vecArr[a].push_back(b);
        vecArr[b].push_back(a);
        
    }
    
    
    for(int i = 0; i<N; i++){
        dfs(i,0);
    }
    
    cout << 0; 				//dfs()에서 즉시 종료 했으므로 depth==4가 있는 경우 해당 코드 실행 x.
    
    return 0;
}

문제 링크 : www.acmicpc.net/problem/10866

문제

정수를 저장하는 덱(Deque)를 구현한 다음, 입력으로 주어지는 명령을 처리하는 프로그램을 작성하시오.

명령은 총 여덟 가지이다.

• push_front X: 정수 X를 덱의 앞에 넣는다.
• push_back X: 정수 X를 덱의 뒤에 넣는다.
• pop_front: 덱의 가장 앞에 있는 수를 빼고, 그 수를 출력한다. 만약, 덱에 들어있는 정수가 없는 경우에는 -1을 출력한다.
• pop_back: 덱의 가장 뒤에 있는 수를 빼고, 그 수를 출력한다. 만약, 덱에 들어있는 정수가 없는 경우에는 -1을 출력한다.
• size: 덱에 들어있는 정수의 개수를 출력한다.
• empty: 덱이 비어있으면 1을, 아니면 0을 출력한다.
• front: 덱의 가장 앞에 있는 정수를 출력한다. 만약 덱에 들어있는 정수가 없는 경우에는 -1을 출력한다.
• back: 덱의 가장 뒤에 있는 정수를 출력한다. 만약 덱에 들어있는 정수가 없는 경우에는 -1을 출력한다.

입력

첫째 줄에 주어지는 명령의 수 N (1 ≤ N ≤ 10,000)이 주어진다. 둘째 줄부터 N개의 줄에는 명령이 하나씩 주어진다. 주어지는 정수는 1보다 크거나 같고, 100,000보다 작거나 같다. 문제에 나와있지 않은 명령이 주어지는 경우는 없다.

출력

출력해야하는 명령이 주어질 때마다, 한 줄에 하나씩 출력한다.

접근 방법

(nanyoungkim.tistory.com/58)  <- 10845번과 비슷한 방식으로 해결했다.

<deque> 라이브러리를 include 해야한다.

@참고 : Deque STL (hyeonstorage.tistory.com/325) 

#include <iostream>
#include <deque>
#include <string>

using namespace std;


int main(){
    
    
    int N;
    cin >> N;
    
    
    deque<int> dque;
    string str;
    int num, res;
    for(int i = 0; i<N; i++){
        
        cin >> str;
        
        if(str=="push_front"){
            cin >> num;
            dque.push_front(num);
        }
        else if(str=="push_back"){
            cin >> num;
            dque.push_back(num);
        }
                
        else if(str=="pop_front"){
            res = dque.empty() ? -1 : dque.front();
            cout << res <<"\n";
            if(!dque.empty()){dque.pop_front();}
        }
        else if(str=="pop_back"){
            res = dque.empty() ? -1 : dque.back();
            cout << res <<"\n";
            if(!dque.empty()){dque.pop_back();}
        }
        
        
        else if(str=="size"){
            cout << dque.size() << "\n";
        }
        else if(str=="empty"){
            res = dque.empty() ? 1 :  0 ;
            cout << res <<"\n";
        }
        else if(str=="front"){
            res = dque.empty() ? -1 : dque.front();
            cout << res << "\n";
        }
        else if(str=="back"){
            res = dque.empty() ? -1 : dque.back();
            cout << res << "\n";
        }
        
    }
    
    
    return 0;
}

문제 링크 : www.acmicpc.net/problem/10845

문제

정수를 저장하는 큐를 구현한 다음, 입력으로 주어지는 명령을 처리하는 프로그램을 작성하시오.

명령은 총 여섯 가지이다.

• push X: 정수 X를 큐에 넣는 연산이다.
• pop: 큐에서 가장 앞에 있는 정수를 빼고, 그 수를 출력한다. 만약 큐에 들어있는 정수가 없는 경우에는 -1을 출력한다.
• size: 큐에 들어있는 정수의 개수를 출력한다.
• empty: 큐가 비어있으면 1, 아니면 0을 출력한다.
• front: 큐의 가장 앞에 있는 정수를 출력한다. 만약 큐에 들어있는 정수가 없는 경우에는 -1을 출력한다.
• back: 큐의 가장 뒤에 있는 정수를 출력한다. 만약 큐에 들어있는 정수가 없는 경우에는 -1을 출력한다.

입력

첫째 줄에 주어지는 명령의 수 N (1 ≤ N ≤ 10,000)이 주어진다. 둘째 줄부터 N개의 줄에는 명령이 하나씩 주어진다. 주어지는 정수는 1보다 크거나 같고, 100,000보다 작거나 같다. 문제에 나와있지 않은 명령이 주어지는 경우는 없다.

출력

출력해야하는 명령이 주어질 때마다, 한 줄에 하나씩 출력한다.

접근 방법 

조건에 맞게 if else문으로 나눠서 풀어주었다. 코드를 좀 더 간단하게 하기 위해 삼항연산자를 사용해보았다.

#include <iostream>
#include <queue>
#include <string>

using namespace std;


int main(){
    
    
    int N;
    cin >> N;
    
    
    queue<int> que;
    string str;
    int num, res;
    for(int i = 0; i<N; i++){
        
        cin >> str;
        
        if(str=="push"){
            cin >> num;
            que.push(num);
        }
        if(str=="pop"){
            if(que.empty()){
                cout << "-1\n";
            }
            else{
                cout << que.front() << "\n";
                que.pop();
            }
        }
        else if(str=="size"){
            cout << que.size() << "\n";
        }
        else if(str=="empty"){
            res = que.empty() ? 1 :  0 ;
            cout << res <<"\n";
        }
        else if(str=="front"){
            res = que.empty() ? -1 : que.front();
            cout << res << "\n";
        }
        else if(str=="back"){
            res = que.empty() ? -1 : que.back();
            cout << res << "\n";
        }
        
    }
    
    
    return 0;
}

문제 링크 : www.acmicpc.net/problem/11722

문제

수열 A가 주어졌을 때, 가장 긴 감소하는 부분 수열을 구하는 프로그램을 작성하시오.

예를 들어, 수열 A = {10, 30, 10, 20, 20, 10} 인 경우에 가장 긴 감소하는 부분 수열은 A = {10, 30, 10, 20, 20, 10}  이고, 길이는 3이다.

입력

첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000)이 주어진다.

둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000)

출력

첫째 줄에 수열 A의 가장 긴 감소하는 부분 수열의 길이를 출력한다.

접근 방법

아래 주석과 같다

#include <iostream>
#include <vector>
using namespace std;

int main() {

	int N; cin >> N;
	vector<int> vec;
	vector<int> vecArr[1000];
	int dp[1001] = { 0 };

	for (int i = 0; i < N; i++) {
		int num; cin >> num;
		vec.push_back(num);
	}
	dp[0] = 1;
	vecArr[0].push_back(vec[0]);


	vector<int> longVec = vecArr[0];
	for (int i = 1; i < vec.size(); i++) {

		vecArr[i].push_back(vec[i]);			//일단 처음에 초기화 해 놓고
		dp[i] = 1;

		
		for (int j = 0; j < i; j++) {			//처음부터 해당 차례 직전까지 돌면서 
			if (vec[i] < vec[j]) {				//해당 차례가 더 작으면 이어 붙인다
				if (dp[j] + 1 > dp[i]) {		//대신 dp 갱신 조건을 만족해야만 이어붙인다
					vecArr[i].clear();
					vecArr[i] = vecArr[j];
					vecArr[i].push_back(vec[i]);
					dp[i] = dp[j] + 1;
				}
			}
		}
		

		if (longVec.size() < vecArr[i].size()) {		//매번 가장 긴 수열을 갱신한다
			longVec = vecArr[i];
		}		
	}


	cout << longVec.size();

	return 0;
}

문제 링크 : www.acmicpc.net/problem/11057

문제

오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.

예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.

수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.

입력

첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.

출력

첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.

접근 방법

dp[N][j] : N자리 수 중 j로 끝나는 수의 개수

로 정의하고 경우의 수를 아래 그림과 같이 나열해보니 쉽게 규칙을 찾을 수 있었다.

문제에서 수는 0으로 시작할 수 있다고 했으므로 이를 주의하자.

dp[1][0], dp[1][1],,, dp[1][9]는 모두 한 자리 수에 해당하므로 1로 초기화하고 N=2부터 dp를 구해준다.

#include <iostream>

using namespace std; 


int main() {

	int dp[1001][10];
	for (int i = 0; i <= 1000; i++) {
		for (int j = 0; j <= 9; j++) {
			dp[i][j] = 0;
		}
	}

	for (int i = 0; i <= 9; i++) {
		dp[1][i] = 1;		//한자리수 초기화	
	}
	for (int i = 0; i <= 1000; i++) {
		dp[i][0] = 1;			//0으로 끝나는 오르막 수는 1개
	}

	for (int i = 2; i <= 1000; i++) {
		for (int j = 1; j <= 9; j++) {
			for (int k = 0; k <= j; k++) {
				dp[i][j] += dp[i - 1][k] % 10007;			//더할때마다 MOD 연산 수행
			}
		}
	}


	int N; 
	cin >> N;

	int ans = 0;
	for (int i = 0; i <= 9; i++) {
		ans += dp[N][i];
	}
	cout << ans % 10007;			//마지막 출력할 때도 MOD 연산 후 출력

	return 0;
}

이때 주의할 점은 ans += dp[N][i] % 10007을 하고 마지막에는 그냥 ans 만 출력하면 틀린 답이라고 나온다는 것이다.

(이론상 mod 연산은 분배법칙이 성립해서 (a mod m + b mod m) = (a+b)mod m 를 만족하는데 왜 틀린지 모르겠다.)

문제 링크 : www.acmicpc.net/problem/1149

문제

RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

• 1번 집의 색은 2번 집의 색과 같지 않아야 한다.
• N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
• i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.

입력

첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

출력

첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.

접근 방법

현재 내가 칠할 색을 r,g,b로 각각 세 경우로 나눠서 생각해야한다.

만약 내가 현재 r을 칠한다고 하면, 그 전 집은 g 또는 b로 칠할 수 있다. 

현재 g를 칠한다고 하면, 그 전 집은 r 또는 b로 칠할 수 있다.

현재 b를 칠한다고 하면, 그 전 집은 r 또는 g로 칠할 수 있다.

dp[i][0] 은 i번째 집을 r로 칠하는 경우에, 1~i번째 집을 모두 칠하는데에 드는 최소 비용을 저장하고

dp[i][1] 은 i번째 집을 g로 칠하는 경우에, 1~i번째 집을 모두 칠하는데에 드는 최소 비용을 저장하고

dp[i][2] 은 i번째 집을 b로 칠하는 경우에, 1~i번째 집을 모두 칠하는데에 드는 최소 비용을 저장한다.

문제의 예제로 생각해보자. 아래 표는 dp[][] 이다.

3번째 집을 칠하기까지 최소 비용은 min(96,172,185) = 96이 답이 된다.

처음에는 3가지가 아닌 6가지로 나눠서 생각했었다. (현재 내가 r을 칠하는 경우에 (전에 g, 전전에 b) or (전에 b, 전전에 g) .... 이런식으로) 

그러나 어짜피 dp[i][0]에 값을 저장할 때, i번째에 r을 칠할 때 

1) i-1 번째 g 칠하기

2) i-1 번째 b 칠하기

이렇게 두가지 경우에서 최소 값을 따져서 저장했으므로 6가지로 나눠서 생각할 필요 없이 3가지로만 나눠서 생각하면 되는 것이다.

#include <iostream>
#include <algorithm>

using namespace std;

int rgbArr[1001][3];
int dp[1001][3];

int main(){
    
    int N; cin>>N;

    for(int i = 1; i<=N; i++){
        for(int j = 0; j<=2; j++){
            scanf("%d", &rgbArr[i][j]);
        }
    }
    rgbArr[0][0] = 0;   rgbArr[0][1] = 0;   rgbArr[0][2] = 0;
    dp[0][0] = 0;   dp[0][1] = 0;   dp[0][2] = 0;
    dp[1][0] = rgbArr[1][0];    dp[1][1] = rgbArr[1][1];    dp[1][2] = rgbArr[1][2];

    
    for(int i = 2; i<=N; i++){
        
        dp[i][0] = min(rgbArr[i][0] + dp[i-1][1], rgbArr[i][0] + dp[i-1][2]);
        dp[i][1] = min(rgbArr[i][1] + dp[i-1][0], rgbArr[i][1] + dp[i-1][2]);
        dp[i][2] = min(rgbArr[i][2] + dp[i-1][0], rgbArr[i][2] + dp[i-1][1]);
        
        int mini=1000000; //1000*1000
        for(int j = 0; j<=2; j++){
            mini = min(mini, dp[i][j]);
        }
        
    }
    
    int ans=1000000;
    for(int i = 0; i<3; i++){
        ans = min(ans, dp[N][i]);
    }

    
    cout << ans;
    return 0;
}