문제 링크 : www.acmicpc.net/problem/11057
11057번: 오르막 수
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다. 예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다. 수
www.acmicpc.net
문제
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.
예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.
수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.
입력
첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.
출력
첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.
접근 방법
dp[N][j] : N자리 수 중 j로 끝나는 수의 개수
로 정의하고 경우의 수를 아래 그림과 같이 나열해보니 쉽게 규칙을 찾을 수 있었다.
문제에서 수는 0으로 시작할 수 있다고 했으므로 이를 주의하자.
dp[1][0], dp[1][1],,, dp[1][9]는 모두 한 자리 수에 해당하므로 1로 초기화하고 N=2부터 dp를 구해준다.
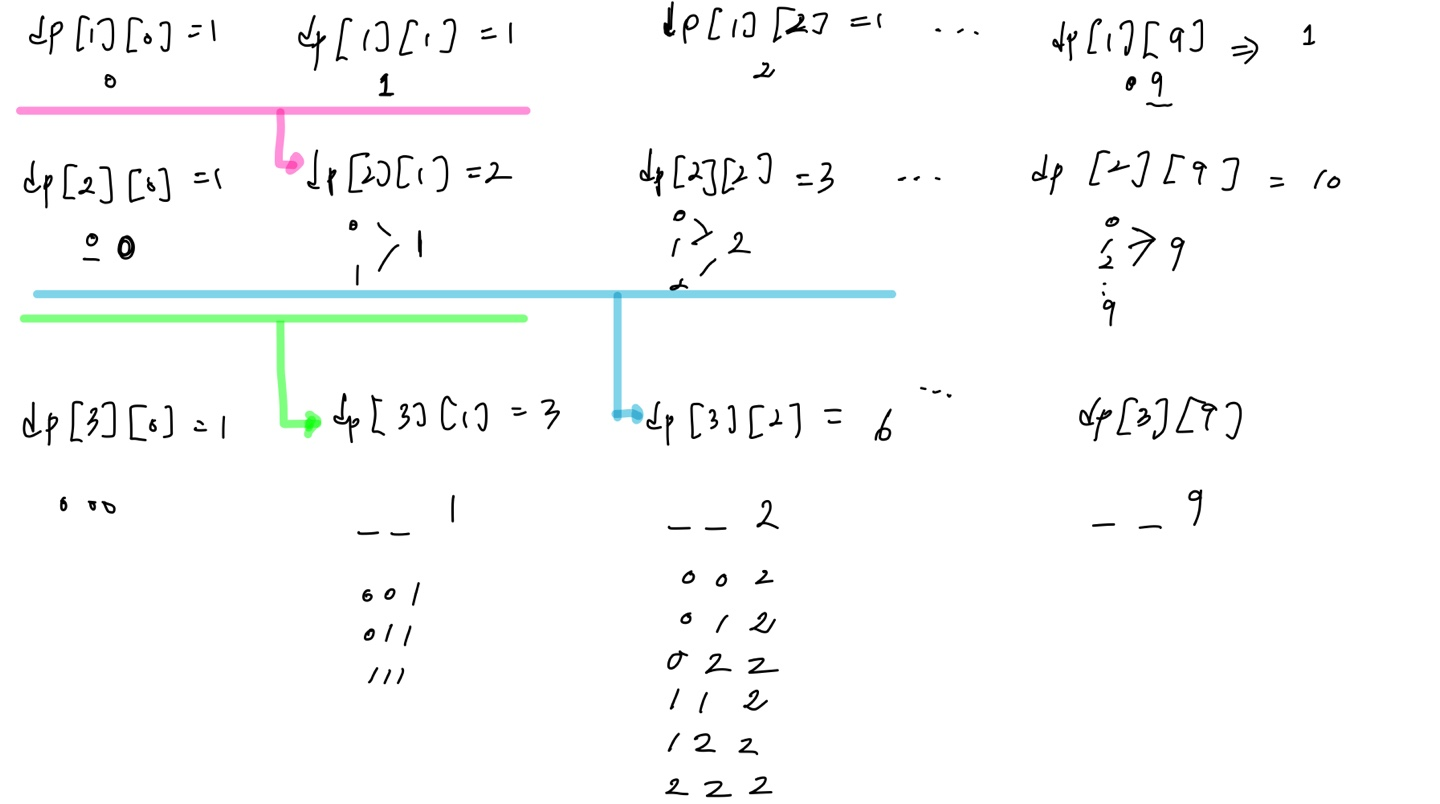
#include <iostream>
using namespace std;
int main() {
int dp[1001][10];
for (int i = 0; i <= 1000; i++) {
for (int j = 0; j <= 9; j++) {
dp[i][j] = 0;
}
}
for (int i = 0; i <= 9; i++) {
dp[1][i] = 1; //한자리수 초기화
}
for (int i = 0; i <= 1000; i++) {
dp[i][0] = 1; //0으로 끝나는 오르막 수는 1개
}
for (int i = 2; i <= 1000; i++) {
for (int j = 1; j <= 9; j++) {
for (int k = 0; k <= j; k++) {
dp[i][j] += dp[i - 1][k] % 10007; //더할때마다 MOD 연산 수행
}
}
}
int N;
cin >> N;
int ans = 0;
for (int i = 0; i <= 9; i++) {
ans += dp[N][i];
}
cout << ans % 10007; //마지막 출력할 때도 MOD 연산 후 출력
return 0;
}이때 주의할 점은 ans += dp[N][i] % 10007을 하고 마지막에는 그냥 ans 만 출력하면 틀린 답이라고 나온다는 것이다.
(이론상 mod 연산은 분배법칙이 성립해서 (a mod m + b mod m) = (a+b)mod m 를 만족하는데 왜 틀린지 모르겠다.)

'Algorithm(BOJ) > DP' 카테고리의 다른 글
| [C++] 백준 2579번 - 계단 오르기 (0) | 2021.04.11 |
|---|---|
| [C++] 백준 11722번 - 가장 긴 감소하는 부분 순열 (0) | 2021.02.26 |
| [C++] 백준 1149번 - RGB 거리 (0) | 2021.02.22 |
| [C++] 백준 1463번 - 1로 만들기 (0) | 2021.02.22 |
| [C++] 백준 1912번 - 연속합 (0) | 2021.02.19 |