문제 링크 : https://www.acmicpc.net/problem/10164
10164번: 격자상의 경로
입력의 첫째 줄에는 격자의 행의 수와 열의 수를 나타내는 두 정수 N과 M(1 ≤ N, M ≤ 15), 그리고 ○로 표시된 칸의 번호를 나타내는 정수 K(K=0 또는 1 < K < N×M)가 차례로 주어지며, 각 값은 공백으
www.acmicpc.net
문제
행의 수가 N이고 열의 수가 M인 격자의 각 칸에 1부터 N×M까지의 번호가 첫 행부터 시작하여 차례로 부여되어 있다. 격자의 어떤 칸은 ○ 표시가 되어 있다. (단, 1번 칸과 N × M번 칸은 ○ 표시가 되어 있지 않다. 또한, ○ 표시가 되어 있는 칸은 최대 한 개이다. 즉, ○ 표시가 된 칸이 없을 수도 있다.)
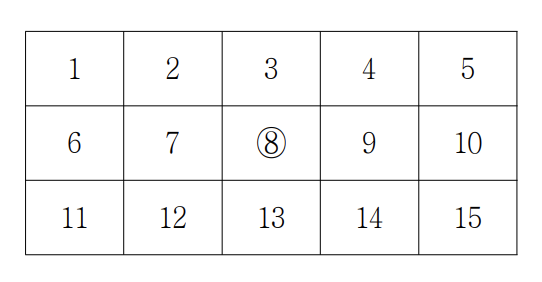
행의 수가 3이고 열의 수가 5인 격자에서 각 칸에 번호가 1부터 차례대로 부여된 예가 아래에 있다. 이 격자에서는 8번 칸에 ○ 표시가 되어 있다.
격자의 1번 칸에서 출발한 어떤 로봇이 아래의 두 조건을 만족하면서 N×M번 칸으로 가고자 한다.
- 조건 1: 로봇은 한 번에 오른쪽에 인접한 칸 또는 아래에 인접한 칸으로만 이동할 수 있다. (즉, 대각선 방향으로는 이동할 수 없다.)
- 조건 2: 격자에 ○로 표시된 칸이 있는 경우엔 로봇은 그 칸을 반드시 지나가야 한다.
위에서 보인 것과 같은 격자가 주어질 때, 로봇이 이동할 수 있는 서로 다른 경로의 두 가지 예가 아래에 있다.
- 1 → 2 → 3 → 8 → 9 → 10 → 15
- 1 → 2 → 3 → 8 → 13 → 14 → 15
격자에 관한 정보가 주어질 때 로봇이 앞에서 설명한 두 조건을 만족하면서 이동할 수 있는 서로 다른 경로가 총 몇 개나 되는지 찾는 프로그램을 작성하라.
입력
입력의 첫째 줄에는 격자의 행의 수와 열의 수를 나타내는 두 정수 N과 M(1 ≤ N, M ≤ 15), 그리고 ○로 표시된 칸의 번호를 나타내는 정수 K(K=0 또는 1 < K < N×M)가 차례로 주어지며, 각 값은 공백으로 구분된다. K의 값이 0인 경우도 있는데, 이는 ○로 표시된 칸이 없음을 의미한다. N과 M이 동시에 1인 경우는 없다.
출력
주어진 격자의 정보를 이용하여 설명한 조건을 만족하는 서로 다른 경로의 수를 계산하여 출력해야 한다.
서브태스크
| 1 | 9 | 1 ≤ N, M ≤ 5, K = 0 |
| 2 | 24 | 1 ≤ N, M ≤ 5, 1 < K < N × M |
| 3 | 23 | 1 ≤ N, M ≤ 15, K = 0 |
| 4 | 44 | 원래의 제약조건 이외에 아무 제약조건이 없다. |
접근 방법
처음에는 조합으로 풀었다가 32점이 나와서 dp로 문제를 해결했다.
처음 접근 방법은 K가 0이 아니면
K의 좌표를 구한 다음 -> 그 좌표까지 가려면 우측 방향으로 몇번 가야하는지와 아래 방향으로 몇 번 가야하는지를 조합을 사용해서 계산햇다.
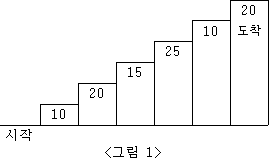
예제를 예시로 들면 아래에서 K까지 가려면 처음 [0][0]에서 우측으로 두 번, 아래 방향으로 한 번 가면 되는 것이다.
총 세번 이동을 해야하는데 그 중에 아래 화살표들을 순서 상관 없이 나열하는 조합의 경우의 수를 구하면 된다.
➡️➡️⬇️
➡️⬇️➡️
⬇️➡️➡️
import java.util.Scanner;
public class Main {
static int combi(int n, int r){
if(n==r || r==0) return 1;
return combi(n-1, r-1) + combi(n-1,r);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int K = sc.nextInt();
int ans = 0;
if(K!=0){
int kRow = K/M;
int kCol = K%M -1;
int first = combi(kRow+kCol, kCol);
int second = combi(M-kCol-1 + N-kRow-1, N-kRow-1);
ans = first*second;
}
else{
ans = combi(N+M-2, N-1);
}
System.out.println(ans);
}
}

그러나 이 방법으로는 32점밖에 안 나와서 N,M이 커지면 서브테스크 3번부터 막히는 것 같아 dp로 다시 풀었다.
dp로 풀때 주의할 점은 K의 위치를 잘 구해야 한다는 것이다.
예제로 주어진 문제로만 푸는 것이 아니라
반레로 K가 M으로 딱 나눠서 떨어지는 경우 즉 입력 값이 (2, 2, 2) 인 케이스도 생각하면 서브 테스크 3,4번도 모두 맞출 수 있다
import java.util.Scanner;
public class BJOJ_10164_격자상의경로 {
static int combi(int n, int r){
if(n==r || r==0) return 1;
return combi(n-1, r-1) + combi(n-1,r);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int M = sc.nextInt();
int K = sc.nextInt();
int ans = 0;
int[][] dp = new int[N][M];
dp[0][0] = 0;
if(K!=0){
int kRow = K/M;
int kCol = K%M;
if(K%M == 0) { //K가 오른쪽 끝에 붙어있는 경우 고려
kRow -= 1;
kCol = M-1;
}else kCol-=1;
for(int i = 1; i<=kRow; i++) {
dp[i][0] = 1;
}
for(int i = 1; i<=kCol; i++){
dp[0][i] = 1;
}
for(int i = 1; i<=kRow; i++){
for(int j = 1; j<=kCol; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
for(int i = kRow+1; i<N; i++) dp[i][kCol] = dp[kRow][kCol];
for(int j = kCol+1; j<M; j++) dp[kRow][j] = dp[kRow][kCol];
for(int i = kRow+1; i<N; i++){
for(int j = kCol+1; j<M; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
else{
for(int i = 1; i<N; i++) {
dp[i][0] = 1;
}
for(int i = 1; i<M; i++){
dp[0][i] = 1;
}
for(int i = 1; i<N; i++){
for(int j = 1; j<M; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
System.out.println(dp[N-1][M-1]);
}
}
'Algorithm(BOJ) > DP' 카테고리의 다른 글
| [Java] 백준 15989번 - 1,2,3 더하기 4 (dp, 다이나믹 프로그래밍) (0) | 2024.03.24 |
|---|---|
| [Java] 백준 9251번 - LCS (0) | 2023.05.07 |
| [C++] 백준 2748번 - 피보나치 수2 (DP, 자료형 주의) (0) | 2021.08.17 |
| [C++] 백준 17069번 - 파이프 옮기기2 (DP, 3차원 배열) (0) | 2021.08.16 |
| [C++] 백준 10942번 - 팰린드롬? (DP, 다이나믹 프로그래밍) (0) | 2021.08.16 |