문제 링크 : https://www.acmicpc.net/problem/17069
17069번: 파이프 옮기기 2
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의
www.acmicpc.net
문제
유현이가 새 집으로 이사했다. 새 집의 크기는 N×N의 격자판으로 나타낼 수 있고, 1×1크기의 정사각형 칸으로 나누어져 있다. 각각의 칸은 (r, c)로 나타낼 수 있다. 여기서 r은 행의 번호, c는 열의 번호이고, 행과 열의 번호는 1부터 시작한다. 각각의 칸은 빈 칸이거나 벽이다.
오늘은 집 수리를 위해서 파이프 하나를 옮기려고 한다. 파이프는 아래와 같은 형태이고, 2개의 연속된 칸을 차지하는 크기이다.

파이프는 회전시킬 수 있으며, 아래와 같이 3가지 방향이 가능하다.

파이프는 매우 무겁기 때문에, 유현이는 파이프를 밀어서 이동시키려고 한다. 벽에는 새로운 벽지를 발랐기 때문에, 파이프가 벽을 긁으면 안 된다. 즉, 파이프는 항상 빈 칸만 차지해야 한다.
파이프를 밀 수 있는 방향은 총 3가지가 있으며, →, ↘, ↓ 방향이다. 파이프는 밀면서 회전시킬 수 있다. 회전은 45도만 회전시킬 수 있으며, 미는 방향은 오른쪽, 아래, 또는 오른쪽 아래 대각선 방향이어야 한다.
파이프가 가로로 놓여진 경우에 가능한 이동 방법은 총 2가지, 세로로 놓여진 경우에는 2가지, 대각선 방향으로 놓여진 경우에는 3가지가 있다.
아래 그림은 파이프가 놓여진 방향에 따라서 이동할 수 있는 방법을 모두 나타낸 것이고, 꼭 빈 칸이어야 하는 곳은 색으로 표시되어져 있다.
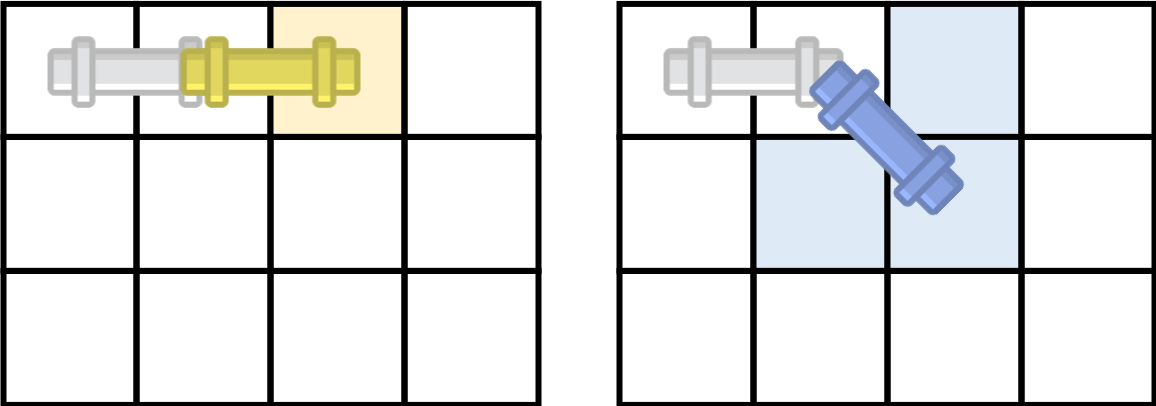
가로

세로
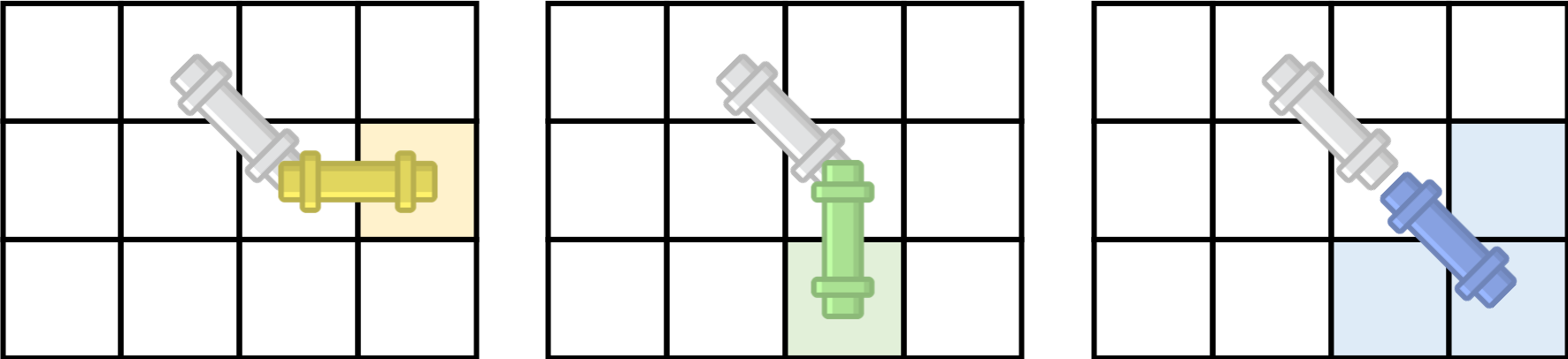
대각선
가장 처음에 파이프는 (1, 1)와 (1, 2)를 차지하고 있고, 방향은 가로이다. 파이프의 한쪽 끝을 (N, N)로 이동시키는 방법의 개수를 구해보자.
입력
첫째 줄에 집의 크기 N(3 ≤ N ≤ 32)이 주어진다. 둘째 줄부터 N개의 줄에는 집의 상태가 주어진다. 빈 칸은 0, 벽은 1로 주어진다. (1, 1)과 (1, 2)는 항상 빈 칸이다.
출력
첫째 줄에 파이프의 한쪽 끝을 (N, N)으로 이동시키는 방법의 수를 출력한다. 이동시킬 수 없는 경우에는 0을 출력한다.
접근 방법
파이프 옮기기1번(https://nanyoungkim.tistory.com/183)
과 문제는 같지만, N 최대값이 16에서 32로 커졌기 때문에 같은 코드로는 시간초과가 났다.
- DP와 삼차원 배열을 이용해서 해결해보자.
- dp[i][r][c] : 파이프 방향이 i이고, 현재 파이프 끝의 위치가 [r][c]일때의 (1,2)부터 (r,c) 로 가는 방법의 수
step 1) 처음 시작 위치 초기화
dp[0][1][2] : 처음 초기 상태로 1을 저장한다.
step 2) 첫 줄 초기화
dp[0][1][3]부터 dp[0][1][N]은 (1,2)에서 시작해서 가로로 쭉 이동하는 경우밖에 없다. 쭉 이동하면서 1로 초기화 하되, 벽이 나타나면 가로로 더 이상 이동할 수 없으므로 중단한다. (벽 오른쪽은 모두 0 인 상태로 남게 됨)
stpe 3) dp 채우기
첫번째 줄은 채웠으니, 두번째 줄과 두번째 열부터 dp를 채운다.
이때 경우는 아래의 3가지로 나눌 수 있다.
(이전위치) -> (현재 위치 & 현재 상태 가로일 때) : 현재(r,c) 상태가 가로이므로 이전 위치는 (r, c-1)이며, 이전 상태는 가로/대각선.
(이전위치) -> (현재 위치 & 현재 상태 세로일 때) : 현재(r,c) 상태가 세로이므로 이전 위치는 (r-1, c)이며, 이전 상태는 세로/대각선.
(이전위치) -> (현재 위치 & 현재 상태 대각선일 때): 현재(r,c) 상태가 대각선이므로 이전 위치는 (r-1,c-1)이며, 이전 상태는 가로/세로/대각선
이 세 경우를 코드로 표현하면 아래와 같다. 세번째 경우는 대각선으로 이동한 경우이므로 (r,c)의 위와 왼쪽도 벽이 아닌지 검사해야한다.
for (int r = 2; r <= N; r++)
{
for (int c = 2; c <= N; c++)
{
if (map[r][c] == 1)
continue;
//가로 -> 가로 , 대각선 -> 가로 : (r,c-1) -> (r,c)
dp[0][r][c] = dp[0][r][c - 1] + dp[2][r][c - 1];
//세로 -> 세로 , 대각선 -> 세로 : (r-1, c) -> (r,c)
dp[1][r][c] = dp[1][r - 1][c] + dp[2][r - 1][c];
//가로 -> 대각선, 세로 -> 대각선 , 대각선 ->대각선 : (r-1, c-0) -> (r,c)
if (map[r - 1][c] != 1 && map[r][c - 1] != 1)
dp[2][r][c] = dp[0][r - 1][c - 1] + dp[1][r - 1][c - 1] + dp[2][r - 1][c - 1];
}
}
전체 코드
//
// BF_BOJ17070_파이프옮기기2.cpp
// Coding_Test_Practice
//
// Created by 김난영 on 2021/08/12.
// Copyright © 2021 KimNanyoung. All rights reserved.
//
#include <iostream>
using namespace std;
int N;
int map[33][33];
long dp[3][33][33];
int main()
{
cin >> N;
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= N; j++)
{
cin >> map[i][j];
}
}
for (int col = 2; col <= N; col++)
{ //(1,2) 에서 오른쪽으로 가로로 쭉 이동
if (map[1][col] == 1)
break;
else
dp[0][1][col] = 1;
}
for (int r = 2; r <= N; r++)
{
for (int c = 2; c <= N; c++)
{
if (map[r][c] == 1)
continue;
//가로 -> 가로 , 대각선 -> 가로 : (r,c-1) -> (r,c)
dp[0][r][c] = dp[0][r][c - 1] + dp[2][r][c - 1];
//세로 -> 세로 , 대각선 -> 세로 : (r-1, c) -> (r,c)
dp[1][r][c] = dp[1][r - 1][c] + dp[2][r - 1][c];
//가로 -> 대각선, 세로 -> 대각선 , 대각선 ->대각선 : (r-1, c-0) -> (r,c)
if (map[r - 1][c] != 1 && map[r][c - 1] != 1)
dp[2][r][c] = dp[0][r - 1][c - 1] + dp[1][r - 1][c - 1] + dp[2][r - 1][c - 1];
}
}
cout << dp[0][N][N] + dp[1][N][N] + dp[2][N][N];
return 0;
}
참고(https://hbj0209.tistory.com/118)
'Algorithm(BOJ) > DP' 카테고리의 다른 글
| [Java] 백준 9251번 - LCS (0) | 2023.05.07 |
|---|---|
| [C++] 백준 2748번 - 피보나치 수2 (DP, 자료형 주의) (0) | 2021.08.17 |
| [C++] 백준 10942번 - 팰린드롬? (DP, 다이나믹 프로그래밍) (0) | 2021.08.16 |
| [C++] 백준 12865번 - 평범한 배낭 (자세한 설명, DP, Knapsadck Problem) (1) | 2021.08.12 |
| [C++] 백준 2579번 - 계단 오르기 (0) | 2021.04.11 |