문제 링크 : www.acmicpc.net/problem/17779
17779번: 게리맨더링 2
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름
www.acmicpc.net
문제
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 재현시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.
재현시는 크기가 N×N인 격자로 나타낼 수 있다. 격자의 각 칸은 구역을 의미하고, r행 c열에 있는 구역은 (r, c)로 나타낼 수 있다. 구역을 다섯 개의 선거구로 나눠야 하고, 각 구역은 다섯 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.
선거구를 나누는 방법은 다음과 같다.
- 기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)
- 다음 칸은 경계선이다.
- (x, y), (x+1, y-1), ..., (x+d1, y-d1)
- (x, y), (x+1, y+1), ..., (x+d2, y+d2)
- (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
- (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)
- 경계선과 경계선의 안에 포함되어있는 곳은 5번 선거구이다.
- 5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.
- 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
- 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
- 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
- 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
아래는 크기가 7×7인 재현시를 다섯 개의 선거구로 나눈 방법의 예시이다.

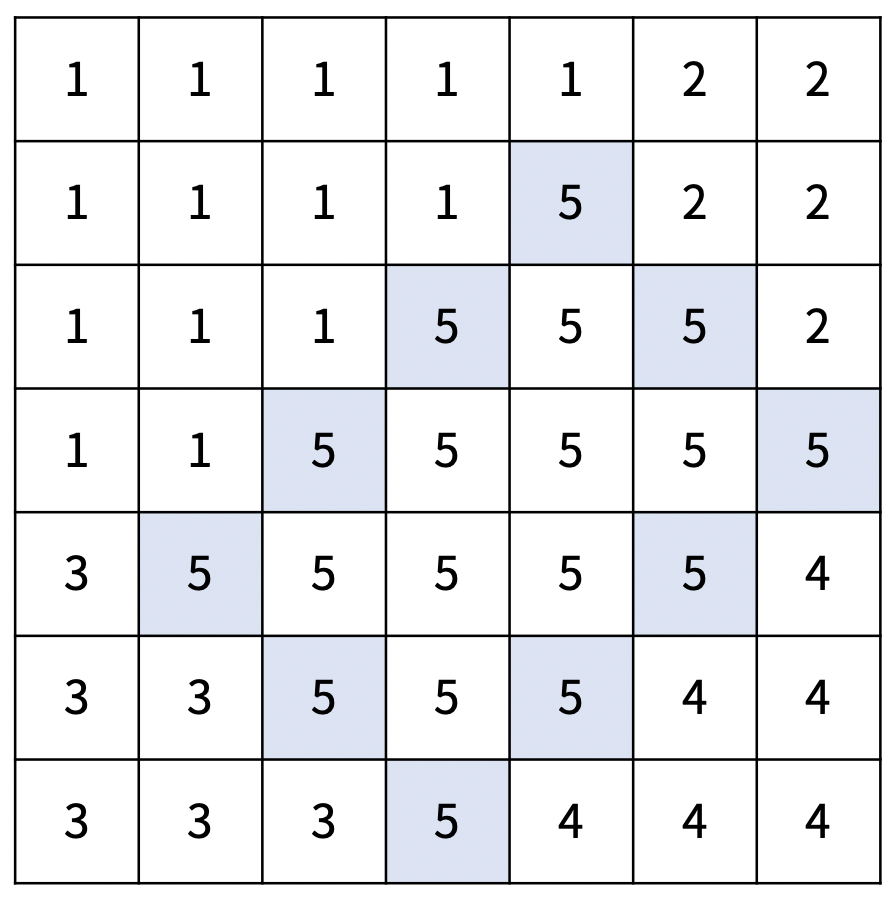

| x = 2, y = 4, d1 = 2, d2 = 2 | x = 2, y = 5, d1 = 3, d2 = 2 | x = 4, y = 3, d1 = 1, d2 = 1 |
구역 (r, c)의 인구는 A[r][c]이고, 선거구의 인구는 선거구에 포함된 구역의 인구를 모두 합한 값이다. 선거구를 나누는 방법 중에서, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구해보자.
입력
첫째 줄에 재현시의 크기 N이 주어진다.
둘째 줄부터 N개의 줄에 N개의 정수가 주어진다. r행 c열의 정수는 A[r][c]를 의미한다.
출력
첫째 줄에 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 출력한다.
제한
- 5 ≤ N ≤ 20
- 1 ≤ A[r][c] ≤ 100
접근 방법
4중 포문을 돌면서 (x,y,d1,d2) 조합을 정한다. (범위 넘어가면 continue 로 넘어간다.)
그렇게 정한 (x,y,d1,d2) 쌍에 대해 아래 순서로 5 선거구역을 표시한다.
1단계 : 5선거구역 표시 => bool divide();
1) (x, y)에서 시작해서 왼쪽 아래 대각선으로 d1만큼 한 번 씩 내려간다. (< v)
2) 한 줄 씩 내려가면서 가로로 y까지 5 선거구역임을 표시한다.
3 )(x, y)에서 시작해서 오른쪽 아래 대각선으로 d2만큼 한 번 씩 내려간다.(> v)
4) 한 줄 씩 내려가면서 y부터 가로로 y까지 5 선거구역임을 표시한다.
5) 위의 1),2)번을 수행한 뒤의 위치부터 다시 오른쪽 대각선 아래로 d2만큼 한 번 씩 이동한다. (> v)
6) 한 줄 씩 내려가면서 가로로 y까지 5 선거구역임을 표시한다.
7) 위의 3),4)번을 수행한 뒤의 위치부터 다시 왼쪽 대각선 아래로 d1만큼 한 번 씩 이동한다. (< v)
8) ) 한 줄 씩 내려가면서 y부터 가로로 y까지 5 선거구역임을 표시한다.
이렇게 하면 5선거구역 표시가 끝난다.
2단계 : 1~4 선거구역 표시 => getpartOne(); getpartTwo(); getpartThree(); getpartFour();
그 다음은 문제에서 주어진 아래의 1~4 선거구역의 범위에 따라
- 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
- 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
- 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
- 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
이미 5선거구역으로 표시되어 있는 곳을 제외하고 해당 선거구역 숫자료 표시해 주면 된다.
#include <iostream>
#include <string.h>
#include <vector>
#include <algorithm>
using namespace std;
int A[21][21];
//위 오 아 왼
int dr[4] = { -1,0,1,0 };
int dc[4] = { 0,1,0,-1 };
int divideMap[21][21];
int N;
//1~N 사이에 들어오는지 범위 체크
bool chk(int r, int c) {
if (r<1 || r>N || c<1 || c>N) return false;
return true;
}
//1~4 선거구역 표시. 5가 이미 표시되어 있는 경우 패스
int getpartOne(int x, int y, int d1, int d2) {
int sum = 0;
for (int i = 1; i < x + d1; i++) {
for (int j = 1; j <= y; j++) {
if (divideMap[i][j] != 5) { //5구역 만나면 다음 줄
divideMap[i][j] = 1;
sum += A[i][j];
}
}
}
return sum;
}
int getpartTwo(int x, int y, int d1, int d2) {
int sum = 0;
for (int i = 1; i <= x + d2; i++) { //1~4
for (int j = y + 1; j <= N; j++) { //6~7
if (divideMap[i][j] != 5) {
divideMap[i][j] = 2;
sum += A[i][j];
}
}
}
return sum;
}
int getpartThree(int x, int y, int d1, int d2) {
int sum = 0;
for (int i = x + d1; i <= N; i++) { //i = 5,6,7
for (int j = 1; j < y - d1 + d2; j++) {
if (divideMap[i][j] != 5) {
divideMap[i][j] = 3;
sum += A[i][j];
}
}
}return sum;
}
int getpartFour(int x, int y, int d1, int d2) {
int sum = 0;
for (int i = x + d2 + 1; i <= N; i++) {
for (int j = y - d1 + d2; j <= N; j++) {
if (divideMap[i][j] != 5) {
divideMap[i][j] = 4;
sum += A[i][j];
}
}
}return sum;
}
//5선거구역 표시. 범위 넘어가서 다른 선거구역의 크기가 최소 1이상 되지 않는 경우 false 리턴
bool divide(int x, int y, int d1, int d2) {
memset(divideMap, 0, sizeof(divideMap));
divideMap[x][y] = 5;
int initR = x;
int initC = y;
//1
for (int k = 0; k < d1; k++) {
int nr = initR + 1;
int nc = initC - 1;
if (!chk(nr, nc)) {
return false;
}
initR = nr;
initC = nc;
for (int col = nc; col <= y; col++) {
divideMap[nr][col] = 5;
}
}
//2
int initR2 = x;
int initC2 = y;
for (int k = 0; k < d2; k++) {
int nr = initR2 + 1;
int nc = initC2 + 1;
if (!chk(nr, nc)) {
return false;
}
initR2 = nr;
initC2 = nc;
for (int col = y; col <= nc; col++) {
divideMap[nr][col] = 5;
}
}
//3
int startR = x + d1;
int startC = y - d1;
for (int k = 0; k < d2; k++) {
int nr = startR + 1;
int nc = startC + 1;
if (!chk(nr, nc)) {
return false;
}
startR = nr;
startC = nc;
for (int col = nc; col <= y - d1 + d2; col++) {
divideMap[nr][col] = 5;
}
}
int startR2 = x + d2;
int startC2 = y + d2;
for (int k = 0; k < d1; k++) {
int nr = startR2 + 1;
int nc = startC2 - 1;
if (!chk(nr, nc)) {
return false;
}
startR2 = nr;
startC2 = nc;
for (int col = y - d1 + d2; col <= nc; col++) {
divideMap[nr][col] = 5;
}
}
return true;
}
int main() {
cin >> N;
int sumA = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cin >> A[i][j];
sumA += A[i][j];
}
}
//각 칸을 돌면서 기준점 정함
int mini = 987654321;
for (int x = 1; x <= N; x++) { //행
for (int y = 1; y <= N; y++) { //열
for (int d1 = 1; d1 <= 18; d1++) {
for (int d2 = 1; d2 <= 18; d2++) {
if (x + d1 + d2 > N) break;
if (!divide(x, y, d1, d2)) continue;
int sum1 = getpartOne(x, y, d1, d2);
int sum2 = getpartTwo(x, y, d1, d2);
int sum3 = getpartThree(x, y, d1, d2);
int sum4 = getpartFour(x, y, d1, d2);
int sum5 = sumA - (sum1 + sum2 + sum3 + sum4);
//각 선거구역 크기는 최소 1칸 이상
if (sum1 >= 1 && sum2 >= 1 && sum3 >= 1 && sum4 >= 1 && sum5 >= 1) {// 선거구는 구역을 적어도 하나 포함해야 하고
vector<int> vec = { sum1, sum2, sum3, sum4, sum5 };
sort(vec.begin(), vec.end());
int maxNum = vec[4];
int minNum = vec[0];
if (mini > maxNum - minNum) mini = maxNum - minNum;
}
}
}
}
}
cout << mini;
return 0;
}
'Algorithm(삼성 코딩테스트 기출)' 카테고리의 다른 글
| [C++] 백준 19237번 - 어른 상어 (구현, 삼성 코테 기출) (0) | 2021.04.23 |
|---|---|
| [C++] 백준 19236번 - 청소년 상어(구현, DFS, 백트래킹) (0) | 2021.04.23 |
| [C++] 백준 17142번 - 연구소 3 (BFS, 중복조합) (0) | 2021.04.22 |
| [C++] 백준 17143번 - 낚시왕 (구현, 시간초과 해결) (0) | 2021.04.21 |