문제 링크 : www.acmicpc.net/submit/11727/26381160
로그인
www.acmicpc.net
문제
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×17 직사각형을 채운 한가지 예이다.

입력
첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)
출력
첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
접근 방법
가로의 길이가 1부터 n이 될 때까지 타일을 붙여나가며, 이때 두가지 케이스로 나눠서 경우의 수를 카운트했다.
붙여야하는 타일의 가로 길이가 1인 것과 2인 것을 나눴다.
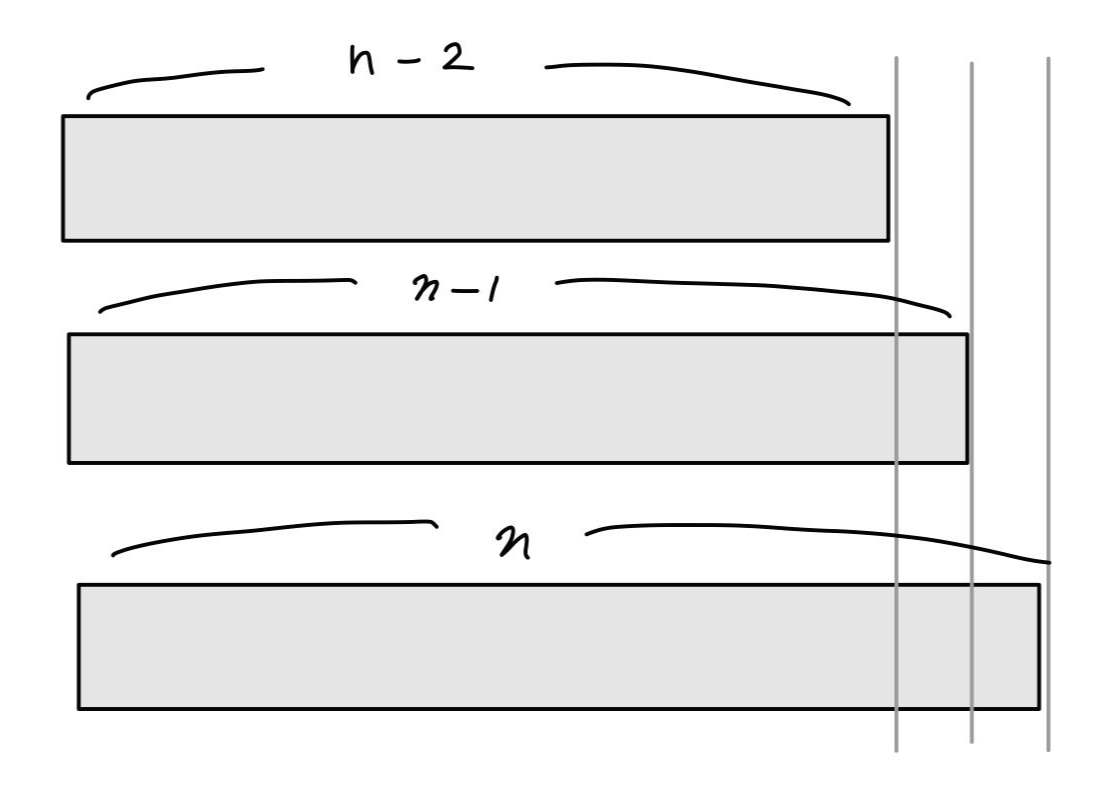
Case 1) 가로 길이가 1인 타일을 붙여야 하는 경우
이 경우는 타일의 길이가 n-1가 되도록 붙이는 경우의 수와 같다. 길이가 n인 타일을 만드려면 n-1 타일에 2x1 타일을 추가하기만 하면 되기 때문이다.
Case 2) 가로 길이가 2인 타일을 붙여야 하는 경우
이 경우엔 두가지 경우로 또 나눠서 생각해야한다.
2-1) 1x2 타일을 붙이는 경우(세로로 두개)
이 경우는 타일의 길이가 n-2가 되도록 붙이는 경우의 수와 같다. 길이가 n인 타일을 만드려면 n-2 타일에 1x2 타일 두개를 세로로 추가하기만 하면 되기 때문이다.
2-2) 2x2 타일을 붙이는 경우
이 경우도 2-1과 같다. 2x2 타일을 추가만 하면 된다.
Case 1, 2를 조합해서 생각하면, 길이 n인 타일을 붙이는 경우의 수는,
길이 n-1인 타일을 붙이는 경우의 수 + 2*(길이 n-2인 타일을 붙이는 경우의 수) 로 나타낼 수 있다.
즉, dp[n] = dp[n-1] + 2*dp[n-2]인 것이다.
#include <iostream>
#include <vector>
using namespace std;
int dp[1001] = {0};
int main(){
int n;
cin >> n;
dp[0] = 0;
dp[1] = 1;
dp[2] = 3;
for(int i = 3; i<=n; i++){
dp[i] = (2*dp[i-2] + dp[i-1]) % 10007;
}
cout << dp[n];
return 0;
}
이때 주의할 점은 for문 안에서 dp[n] = dp[n-1] + 2*dp[n-2] 로 계산을 쭉 하고
마지막에 출력할 때 dp[n]%10007 을 하면 안된다는 것이다. 위의 코드와 같이 for문 안에서 나머지 계산을 해줘야한다.
문제 요구조건 자체가 mod 연산을 한 결과를 출력하라고 했으니, 처음에 dp[]에 값을 저장할 때 mod연산의 결과를 저장해야한다.
'Algorithm(BOJ) > DP' 카테고리의 다른 글
| [C++] 백준 1463번 - 1로 만들기 (0) | 2021.02.22 |
|---|---|
| [C++] 백준 1912번 - 연속합 (0) | 2021.02.19 |
| [C++] 백준 1699번 - 제곱수의 합 (0) | 2021.02.16 |
| [C++] 백준 15990번 - 1,2,3 더하기 5 (0) | 2021.02.15 |
| [C++] 백준 11052번 - 카드 구매하기 (0) | 2021.02.15 |